$$ \begin{cases} v_0 &= 6.00\times10^6\ut{m/s} \\ a &= -1.25\times10^{14}\ut{m/s^2} \\ v &= 0 \end{cases} $$
(a) $$ S =? $$ $$ 2aS = v^2-v_0^2 ,$$ $$ \begin{aligned} \Ans &= S = \frac{v^2-v_0^2}{2a} \\ &= \frac{0^2-(6.00\times10^6\ut{m/s})^2}{2(-1.25\times10^{14}\ut{m/s^2})} \\ &= \frac{18}{125}\ut{m} \\ &= 0.144\ut{m} = 14.4\ut{cm} \end{aligned} $$
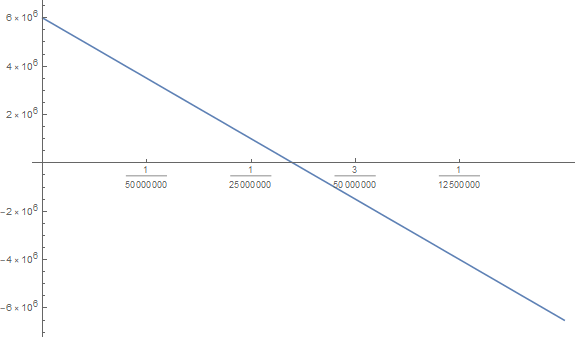
(b) $$ \begin{aligned} x(t) &= v_0t+\frac{1}{2}at^2 \\ &= (6.00\times10^6)t+\frac{1}{2}(-1.25\times10^{14})t^2 \\ &= (6.00\times10^6)t+(-6.25\times 10^{13})t^2 \end{aligned} $$ $$ \begin{aligned} v(t) &= \dot x = \dxt{x} \\ &= \dt\{ (6.00\times10^6)t+(-6.25\times 10^{13})t^2 \} \\ &= 6.00\times10^6 - (1.25\times10^{14})t \end{aligned} $$

'10판 > 2. 직선운동' 카테고리의 다른 글
| 2-28 할리데이 10판 솔루션 일반물리학 (0) | 2019.07.24 |
|---|---|
| 2-27 할리데이 10판 솔루션 일반물리학 (0) | 2019.07.24 |
| 2-25 할리데이 10판 솔루션 일반물리학 (0) | 2019.07.24 |
| 2-24 할리데이 10판 솔루션 일반물리학 (0) | 2019.07.24 |
| 2-23 할리데이 10판 솔루션 일반물리학 (0) | 2019.07.24 |