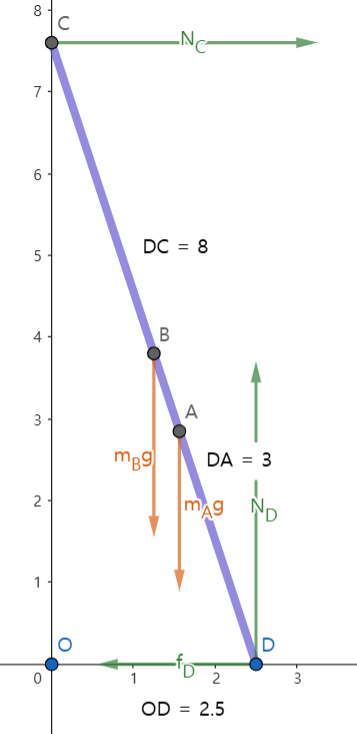
$$ \begin{cases}
m_A&=85\ut{kg}\\
m_B&=10\ut{kg}\\
M&=\Sigma m= 95\ut{kg}\\
\end{cases} $$
$$ \begin{cases}
\Sigma F_{x}&=0\\
\Sigma F_{y}&=0\\
\Sigma \tau_{D}&=0\\
\end{cases} $$
$$ \begin{cases}
0&=N_C-f_D\\
0&=N_D-Mg\\
0&=\br{x_{AD}}m_Ag+\br{x_{BD}}m_Bg-\br{y_{CD}}N_C\\
\end{cases} $$
$$ \begin{cases}
x_{AD}&={L_{AD}\over L_{CD}}x_{OD}\\
x_{BD}&={1\over 2}x_{OD}\\
y_{CD}&=\sqrt{{L_{CD}}^2-{x_{OD}}^2}\\
\end{cases} $$
$$\ab{a}$$
$$ \begin{aligned}
N_C
&={x_{OD}\over y_{CD}}\cdot\br{{L_{AD}\over L_{CD}}m_A+{m_B\over 2}}g\\
&={x_{OD}\over \sqrt{{L_{CD}}^2-{x_{OD}}^2}}\cdot\br{{L_{AD}\over L_{CD}}m_A+{m_B\over 2}}g\\
&={1475\over8\sqrt{231}}g\\
&\approx 118.96431792914245\ut{N}\\
&\approx 1.2\times10^2\ut{N}\\
\end{aligned} $$
$$\ab{b,c}$$
$$ \begin{cases}
f_D&=N_C\\
N_D&=Mg\\
\end{cases} $$
$$ \begin{aligned}
\vec F_D
&=f_D\i+N_D\j\\
&=N_C\i+Mg\j\\
\end{aligned} $$
$$\ab{b}$$
$$ \begin{aligned}
F_D
&=\sqrt{{N_C}^2+\br{Mg}^2}\\
&=g \sqrt{M^2+\br{x_{OD}\over y_{CD}}^2\br{{L_{AD}\over L_{CD}}m_A+{m_B\over2}}^2}\\
&=\frac{5 }{8}\sqrt{\frac{5424049}{231}}g\\
&\approx 939.1965856775718\ut{N}\\
&\approx 9.4\times10^2\ut{N}\\
\end{aligned} $$
$$\ab{c}$$
$$ \begin{aligned}
\theta
&=\tan^{-1}{Mg\over N_C}\\
&=\tan^{-1}{M\over {x_{OD}\over y_{CD}}\cdot\br{{L_{AD}\over L_{CD}}m_A+{m_B\over 2}}}\\
&=\tan^{-1}{152\sqrt{231}\over295}\\
&\approx 1.4437891006369301\ut{rad}\\
&\approx 1.4\ut{rad}\\
\end{aligned} $$

