(풀이자 주 : 그래프의 함수가 정확히 주어지지 않아 풀이자가 임의로 그래프의 함수를 추정했습니다. 추정함수가 다를 경우 결과는 달라질 수 있습니다.) $$\put \exp(x)=\e^x,$$ $$ \put U(x)=\begin{cases} (x-2)^2&\cdots(x\le2)\\ \exp\(\cfrac{3x-6}{10}\)-1&\cdots(x\ge2)\\ \end{cases} $$
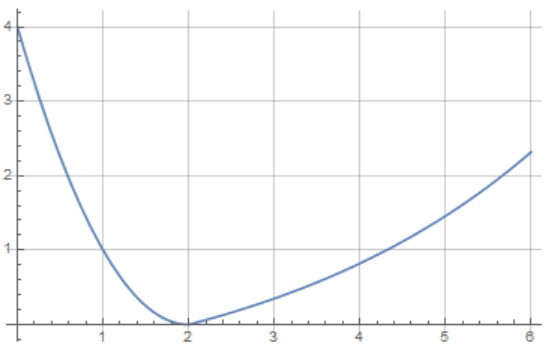
$$\ab{a}$$ $$ \begin{aligned} W_{i\rarr f}&=-\Delta U_{i\rarr f},\\ \int_2^{x} F\dd x&=U_2-U_x\\ \dx\(\int_2^x F\dd x\)&=\dx\(U_2-U_x\)\\ F(x)&=-\dyx{U(x)}, \end{aligned} $$ $$ U(x)=\begin{cases} (x-2)^2&\cdots(x\le2)\\ \exp\(\cfrac{3x-6}{10}\)-1&\cdots(x\ge2)\\ \end{cases} $$ $$ -\dyx{U(x)}=\begin{cases} -\cfrac{\dd}{\dd x}\bra{(x-2)^2}&\cdots(x\le2)\\ -\cfrac{\dd}{\dd x}\bra{\exp\(\cfrac{3x-6}{10}\)-1}&\cdots(x\ge2)\\ \end{cases} $$ $$ F(x)=\begin{cases} -2(x-2)&\cdots(x\le2)\\ -\cfrac{3}{10}\exp\(\cfrac{3x-6}{10}\)&\cdots(x\ge2)\\ \end{cases} $$

$$\ab{b}$$ $$ \begin{aligned} E &= K + U,\\ K&= E-U\\ &=4-U \end{aligned} $$ $$ U(x)=\begin{cases} (x-2)^2&\cdots(x\le2)\\ \exp\(\cfrac{3x-6}{10}\)-1&\cdots(x\ge2)\\ \end{cases} $$ $$ 4-U(x)=\begin{cases} 4-(x-2)^2&\cdots(x\le2)\\ 4-\exp\(\cfrac{3x-6}{10}\)-1&\cdots(x\ge2)\\ \end{cases} $$ $$ K(x)=\begin{cases} 4x-x^2&\cdots(x\le2)\\ 5-\exp\(\cfrac{3x-6}{10}\)&\cdots(x\ge2)\\ \end{cases} $$

'11판 > 8. 퍼텐셜에너지와 에너지 보존' 카테고리의 다른 글
| 8-46 할리데이 11판 솔루션 일반물리학 (0) | 2024.04.04 |
|---|---|
| 8-45 할리데이 11판 솔루션 일반물리학 (0) | 2024.04.04 |
| 8-43 할리데이 11판 솔루션 일반물리학 (0) | 2024.04.04 |
| 8-42 할리데이 11판 솔루션 일반물리학 (0) | 2024.04.04 |
| 8-41 할리데이 11판 솔루션 일반물리학 (0) | 2024.04.03 |