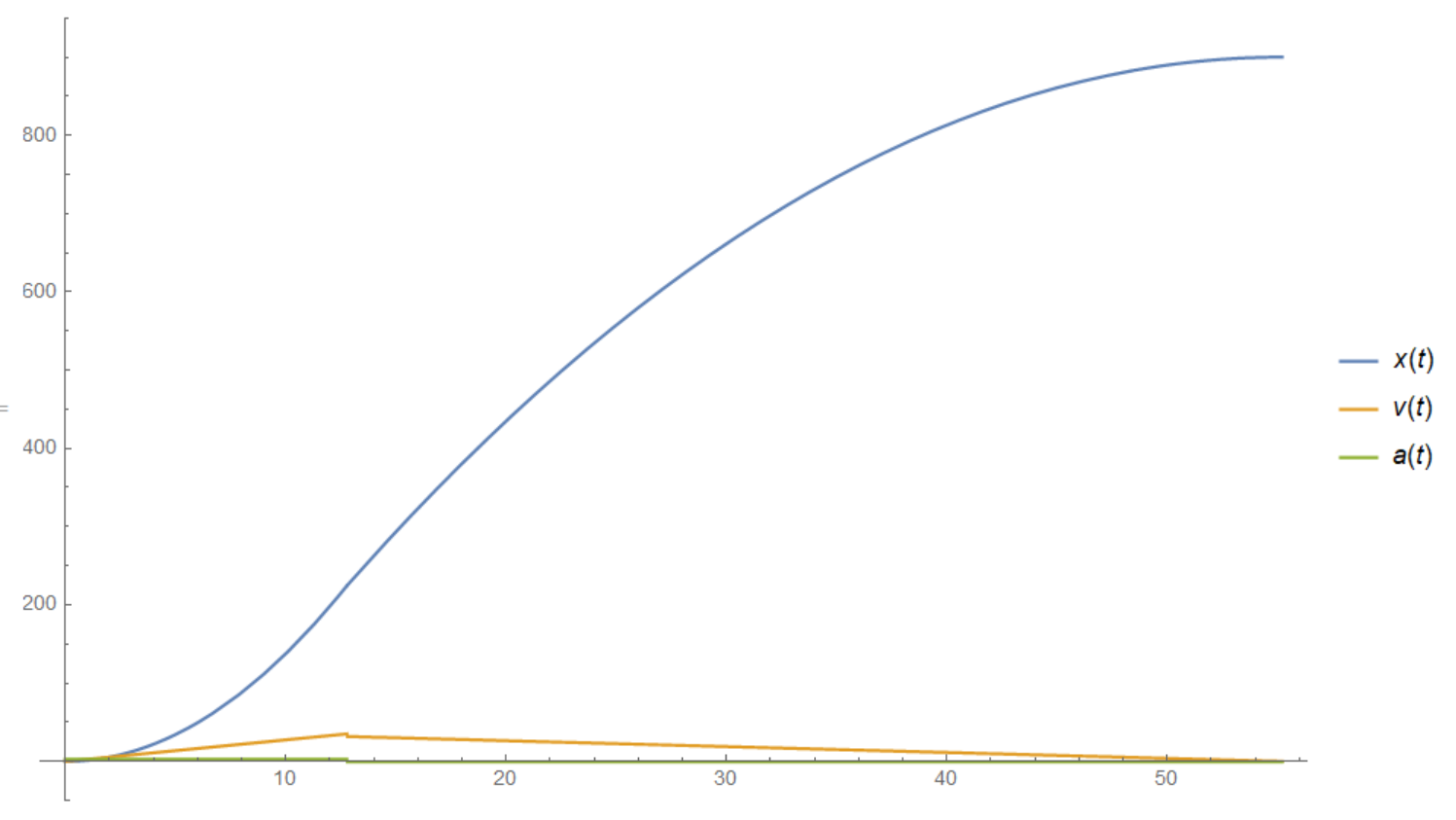
[풀이자주 : 이 문제의 모든 조건을 만족시키면 두 구간이 만나는 시점의 속도가 일치하지 않습니다. (최하단 그래프 참고)
1. 출발지 or 도착지에서 정지하지 않았거나,
2. 구간이 1:3분할이 아니거나,
3. 주어진 가속도가 오차 혹은 틀렸거나
4. 구간변경시점에 무한대의 가속으로 속도가 점프했거나(=물리적으로 불가능)
중 하나입니다.
물리적으로 불가능하지만, 모든 주어진 조건이 참이라고 가정하고 풀었습니다. 위의 4번가능성인 양쪽에서 구한 속도가 구간변경시점에 일치하지 않을 수 있다, 즉, 무한대의 가속도로 속도가 순간변화했다는 가정을 한 것입니다. 만일 위의 다른 가정하에 푼다면 답은 달라집니다. 주의바랍니다.]
[조금만 기하적으로 해석해보면 vt그래프 기준으로 밑넓이가 이동거리이므로, 넓이비가 1:3이며 높이가 같으려면 필수적으로 시간비도 1:3이 되어야 하며, 기울기비는 자동으로 3:1이 되어야 합니다. 하지만 주어진 기울기비는 11:3이죠. 다시말해 거리비(=넓이비)가 3:11 이되거나, 기울기비가 1:3이 되면 조건이 맞을 수 있습니다. 혹은 출발or도착지점에서 정지하지 않았다고 가정하는 방법도 있겠네요.]
덕분에 뭐가 틀렸나 찾느라 개고생했네요 ㅜㅠ
$$\begin{cases} v_0 &= 0 \\ v_4 &= 0 \\ x_0 &= 0 \\ x_4 &= 900\ut{m} \\ x_1 &= \frac{1}{4}x_4 = \frac{900}{4} = 225\ut{m} \\ \Delta x_{1\to4} &= \frac{3}{4}x_4 = \frac{3}{4}900 = 675\ut{m} \\ a_{0\to1} &= +2.75 \ut{m/s^2} \\ a_{1\to4} &= -0.750 \ut{m/s^2} \end{cases} $$
(a) $$t_4 =?$$ $$ \begin{aligned} \Delta x &= v_0t+\frac{1}{2}at^2, \\ \Delta x_{0\to1} &= v_0t_{0\to1}+\frac{1}{2}a_{0\to1}t_{0\to1}^2 \\ x_1-x_0 &= \frac{1}{2}a_{0\to1}(t_1-t_0)^2 \\ x_1 &= \frac{1}{2}a_{0\to1}t_1^2 \cdots(2-36-1) \\ t_1 &= \sqrt{\frac{2x_1}{a_{0\to1}}} \cdots({2-36-2}) \end{aligned} $$ $$ \begin{aligned} \Delta x &= vt-\frac{1}{2}at^2, \\ \Delta x_{1\to4} &= v_4t_{1\to4}-\frac{1}{2}a_{1\to4}t_{1\to4}^2 \\ &= -\frac{1}{2}a_{1\to4}t_{1\to4}^2 \cdots(2-36-3) \end{aligned} $$ $$ \begin{aligned} t_{1\to4}^2 &= - \frac{2\Delta x_{1\to4}}{a_{1\to4}} \\ t_4-t_1 &= \sqrt{- \frac{2\Delta x_{1\to4}}{a_{1\to4}}} \ (\because t\ge 0) \end{aligned} $$ $$ \begin{aligned} \Ans &=t_4 = t_1+\sqrt{- \frac{2\Delta x_{1\to4}}{a_{1\to4}}} \\ &= \sqrt{\frac{2x_1}{a_{0\to1}}} +\sqrt{- \frac{2\Delta x_{1\to4}}{a_{1\to4}}} \\ &= \sqrt{\frac{2(225\ut{m})}{+2.75 \ut{m/s^2}}}+ \sqrt{-\frac{2(675\ut{m})}{-0.750 \ut{m/s^2}}} \\ &= 60 \sqrt{\frac{6}{11}+\frac{1}{\sqrt{11}}}\ut{s}\cdots(2-36-4) \\ &\approx 55.21844985252948\ut{s} \\ &\approx 55.2\ut{s} \end{aligned} $$
(b) $$\max v = v_M = v_1? $$ $$ \begin{aligned} 2a\Delta x &= v^2-v_0^2, \\ 2a_{0\to 1}\Delta x_{0\to 1} &= v_1^2-v_0^2 \end{aligned} $$ $$ \begin{aligned} v_1 &= \sqrt{2a_{0\to 1}(x_1-x_0)} \\ &= \sqrt{2a_{0\to 1}x_1} \\ &= \sqrt{2(+2.75 \ut{m/s^2})(225\ut{m})} \\ &= 15 \sqrt{\frac{11}{2}}\ut{m/s} \\ &\approx 35.17811819867573\ut{m/s} \\ &\approx 35.2\ut{m/s} \end{aligned} $$
(c) $$(2-36-2), $$ $$ \begin{aligned} t_1 &= \sqrt{\frac{2x_1}{a_{0\to1}}} \\ &= \sqrt{\frac{2(225\ut{m})}{+2.75 \ut{m/s^2}}} \\ &= 30 \sqrt{\frac{2}{11}}\ut{s} \end{aligned} $$ $$ \text{(Case A)} $$ $$t<t_1$$ $$ (2-36-1),$$ $$ \begin{aligned} \Delta x_{0\to 1} &=\frac{1}{2}a_At_{0\to 1}^2 \\x(t)-x_0&=\frac{1}{2}a_A(t-t_0)^2 \\x(t)&= \frac{1}{2}(2.75)t^2 \\&=\frac{11}{8}t^2, &(t < t_1) \end{aligned} $$ $$ \begin{aligned} v(t) &= \dot x = \dxt{x} \\&=\dt\left(\frac{11}{8}t^2\right) \\&=\frac{11}{4}t, &(t < t_1) \end{aligned} $$ $$ a(t) = \dot v = \dxt{v} $$ $$ \begin{aligned} a(t)&=\dt \left(\frac{11}{4}t \right) \\&=\frac{11}{4}, &(t < t_1) \end{aligned} $$ $$ \text{(Case B)} $$ $$t>t_1$$ $$ (2-36-3), $$ $$ \begin{aligned} \Delta x_{1\to 4} &= -\frac{1}{2}a_Bt_{1\to 4}^2 \\ x_4-x(t) &= -\frac{1}{2}a_B(t_4-t)^2 \end{aligned} $$ $$(2-36-4),$$ $$ \begin{aligned} x(t)&=900+ \frac{1}{2}(-0.750)\left(60 \sqrt{\frac{6}{11}+\frac{1}{\sqrt{11}}}-t\right)^2 \\ &=900-\frac{3}{8} \left(60\sqrt{\frac{6}{11}+\frac{1}{\sqrt{11}}}-t\right)^2,&(t>t_1) \end{aligned} $$ $$ \begin{aligned} v(t) &= \dot x = \dxt{x} \\ &=\dt\left\{900-\frac{3}{8} \left(60\sqrt{\frac{6}{11}+\frac{1}{\sqrt{11}}}-t\right)^2\right\} \\ &=\frac{3}{4} \left(60\sqrt{\frac{6}{11}+\frac{1}{\sqrt{11}}}-t\right),&(t > t_1) \end{aligned} $$ $$ \begin{aligned} a(t) &= \dot v = \dxt{v} \\&=\dt \left\{ \frac{3}{4} \left( 60\sqrt{\frac{6}{11}+\frac{1}{\sqrt{11}}}-t \right) \right\} \\&=-\frac{3}{4}, &(t > t_1) \end{aligned} $$ $$ \mathbf{\text{주의}} \begin{cases} v(t_1)_{0 \to 1} &= 15 \sqrt{\frac{11}{2}} \approx 35.2, \\ v(t_1)_{1 \to 4} &= \frac{45}{\sqrt{2}} \approx 31.8 \\ \therefore v(t_1)_{0 \to 1} &\ne v(t_1)_{1 \to 4} \end{cases}$$


'10판 > 2. 직선운동' 카테고리의 다른 글
| 2-38 할리데이 10판 솔루션 일반물리학 (0) | 2019.07.25 |
|---|---|
| 2-37 할리데이 10판 솔루션 일반물리학 (0) | 2019.07.25 |
| 2-35 할리데이 10판 솔루션 일반물리학 (0) | 2019.07.25 |
| 2-34 할리데이 10판 솔루션 일반물리학 (0) | 2019.07.25 |
| 2-33 할리데이 10판 솔루션 일반물리학 (0) | 2019.07.25 |