$$\begin{cases} A = \text{Speed Train} \\ B = \text{Slow Train} \\ t_1 = \text{A,B Minimum Distance Time} \\ \end{cases}$$ $$\begin{aligned} v_{A0} &= 161\ut{km/h} \\ &= 161\ut{km/h}\cdot\frac{1000\ut{m}}{1\ut{km}}\cdot\frac{1\ut{h}}{3600\ut{s}} \\ &= \frac{805}{18}\ut{m/s} \\ \end{aligned}$$ $$\begin{aligned} v_B &= 29.0\ut{km/h} \\ &= 29.0\ut{km/h}\cdot\frac{1000\ut{m}}{1\ut{km}}\cdot\frac{1\ut{h}}{3600\ut{s}} \\ &= \frac{145}{18}\ut{m/s} \\ \end{aligned}$$ $$\begin{cases} v_{A0} = \frac{805}{18}\ut{m/s} \\ v_B = \frac{145}{18}\ut{m/s} \\ x_{B0} = 676\ut{m} \\ a < 0 \\ \end{cases}$$
(a) $\forall t>0\Rightarrow x_{B1}>x_{A1},\abs{a}=?$ $$\begin{aligned}\tag{2-43-1} \Delta x&=vt,\\ x_{B0\to1}&=v_Bt_{0\to1}\\ x_{B1}-x_{B0}&=v_Bt_1\\ x_{B1}&=x_{B0}+v_Bt_1\\ \end{aligned}$$ $$\begin{aligned}\tag{2-43-2} \Delta x &= v_0t+\frac{1}{2}at^2,\\ \Delta x_{A0\to1} &= v_{A0}t_{0\to1}+\frac{1}{2}at_{0\to1}^2\\ x_{A1} &= v_{A0}t_1+\frac{1}{2}at_1^2\\ \end{aligned}$$ $$\begin{aligned} x_{B1}&>x_{A1} \quad \\ x_{B0}+v_Bt_1&>v_{A0}t_1+\frac{1}{2}at_1^2\\ 0&>v_{A0}t_1+\frac{1}{2}at_1^2-x_{B0}-v_Bt_1\\ 0&>\frac{1}{2}at_1^2+(v_{A0}-v_B)t_1-x_{B0}\\ \end{aligned}$$ $$ \therefore \frac{1}{2}a<0 \ \& \ D<0$$ $$\begin{aligned} D&=b^2-4ac\\ &=(v_{A0}-v_B)^2-4\(\frac{1}{2}a\)(-x_{B0})\\ &=\(\frac{805}{18}-\frac{145}{18}\)^2-2a\(-676\)\\ &=\frac{12100}{9}+1352a<0 \end{aligned}$$ $$\begin{aligned} a<& -\frac{3025}{3042}\ut{m/s^2}\\ &\approx-0.9944115713346483\ut{m/s^2}\\ &\approx-0.994\ut{m/s^2}\\ \end{aligned}$$ $$\therefore \abs{a}>0.994\ut{m/s^2}$$
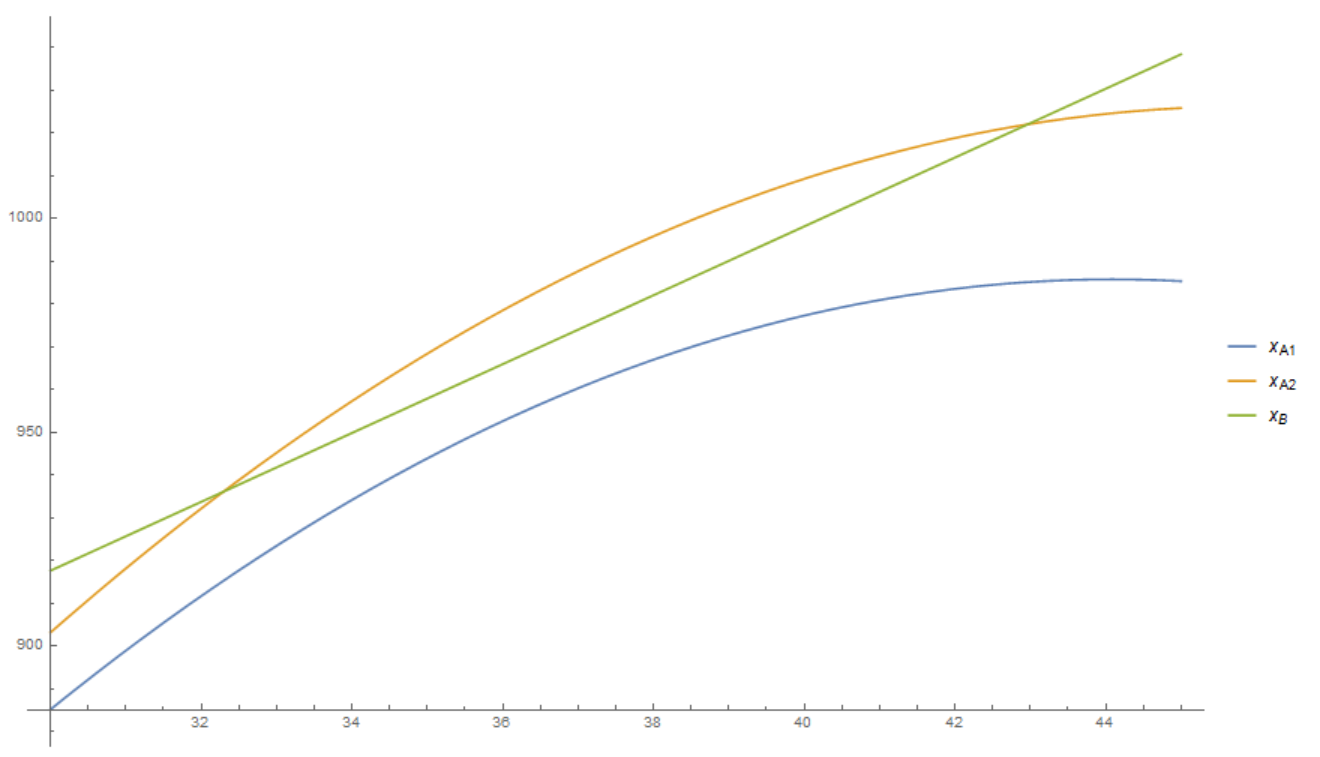
(b) $$ (2-43-2),$$ $$\begin{aligned} x_A(t)&=\frac{805}{18}t+\frac{1}{2}\(-\frac{3025}{3042}\)t^2\\ &=\frac{805}{18}t-\frac{3025}{6084}t^2\\ \end{aligned}$$ $$ (2-43-1),$$ $$x_B(t)=676+\frac{145}{18}t$$

'10판 > 2. 직선운동' 카테고리의 다른 글
| 2-45 할리데이 10판 솔루션 일반물리학 (0) | 2019.07.30 |
|---|---|
| 2-44 할리데이 10판 솔루션 일반물리학 (0) | 2019.07.30 |
| 2-42 할리데이 10판 솔루션 일반물리학 (0) | 2019.07.30 |
| 2-41 할리데이 10판 솔루션 일반물리학 (0) | 2019.07.30 |
| 2-40 할리데이 10판 솔루션 일반물리학 (0) | 2019.07.27 |